Mathematics : চতুর্ভুজ ও তার বিভিন্ন ধর্ম ( Understanding quadrilaterals) Short Question : Class-8

চতুর্ভুজ ও তার বিভিন্ন ধর্ম ( Understanding quadrilaterals)

Class- VIII ( Mathematics )

1) বহুভুজ কাকে বলে?

Ans: তিন বা ততোধিক সরলরেখাংশ দ্বারা সীমাবদ্ধ সামতলিক চিত্রকে বহুভুজ বলে।

2) কর্ণ কি?

Ans : ক্রমিক নয় এরূপ দুটি বিন্দুর সংযোজক রেখাংশকে কর্ণ বলে।

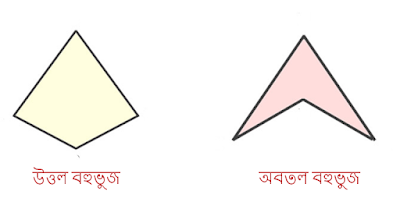
3) উত্তল বহুভুজ এবং অবতল বহুভুজ কাকে বলে? চিত্র এঁকে দেখাও।

Ans : যে সমস্ত বহুভুজের কর্ণ গুলো বহুভুজের ভিতরে অবস্থিত হয়, তাকে উত্তল বহুভুজ বলে। 

     যে সমস্ত বহুভুজের কর্ণ গুলোর কোনও একটি অংশ বহুভুজের বহিঃস্থ হয়, তাদের অবতল বহুভূজ।

4) সুষম বহুভুজ কাকে বলে ? উদাহরণ দাও?

Ans :  যে বহুভুজের প্রতিটি বাহু এবং প্রতিটি কোণ সমান থাকে তাকে সুষম বহুভুজ বলে। যেমন : সমবাহু ত্রিভুজ এবং বর্গক্ষেত্র। 

5) বিষম বহুভুজ কাকে বলে? উদাহরণ দাও।

Ans :  যে বহুভুজের প্রতিটি বাহু এবং প্রতিটি কোণ সমান থাকে না তাদের বিষম বহুভুজ বলে । যেমন - সমকোণী ত্রিভুজ এবং আয়তক্ষেত্র।

6) ত্রিভুজের তিনটি কোণের সমষ্টি কত?

Ans :  180°

7)চতুর্ভুজের চারটি কোণের সমষ্টি কত?

Ans: 360°

8) কোন বহুভুজের বহিঃস্থ কোণগুলোর সমষ্টি কত?

Ans : Ans: 360°

9) একটি উত্তল চতুর্ভুজের কোনগুলি সমষ্টি কত?

Ans: 360°

10) যদি চতুর্ভুজটি উত্তল না হয় তবে কোণের সমষ্টির ধর্ম বজায় থাকবে কি?

Ans : হ্যাঁ ।

11) n-সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্ত:কোণের সমষ্টি কত?

Ans : ( n-2)x180° , যেখানে n = হল বাহুর সংখ্যা।

 12) 10 বাহু বিশিষ্ট বহুভুজের অন্ত:কোণের সমষ্টি কত?

Ans :  n-বাহু বিশিষ্ট বহুভুজের অন্ত:কোণের সমষ্টি = ( n-2)x180° , যেখানে n = হল বাহুর সংখ্যা।

= (10-2)x180°  [ এখানে n = 10 ]

= 8 x 180°

= 1440°

13) তিন বাহু বিশিষ্ট একটি সুষম বহুভুজের উদাহরণ দাও?

Ans : সমবাহু ত্রিভুজ।

14) চার বাহু বিশিষ্ট একটি সুষম বহুভুজের উদাহরণ দাও?

Ans : বর্গক্ষেত্র।

15) 6 বাহু বিশিষ্ট সুষম বহুভুজের নাম লিখ?

Ans : সুষম ষড়ভুজ।

16) উত্তল চতুর্ভুজের কয়টি কর্ণ?

Ans : 2 টি।

17) সুষম ষড়ভুজের কয়টি কর্ণ?

Ans : 9 টি।

18) ত্রিভুজের কর্ণের সংখ্যা কত?

Ans : 0।

19) একটি চতুর্ভুজের চারটি কোণ যথাক্রমে 50° , 130° , 120°  এবং x হলে, x-এর মান কত?

Ans : আমরা জানি, চতুর্ভুজের চারটি কোণের সমষ্টি 360°

সুতরাং  50° + 130° + 120°  + x = 360°

বা, 300° +  x = 360°

বা,   x = 360° - 300° = 60°

20) একটি পঞ্চভুজের পাঁচটি কোণ যথাক্রমে 80° , 130° , 120°,110°  এবং x হলে, x-এর মান কত?

Ans : আমরা জানি, পঞ্চভুজের পাঁচটি কোণের সমষ্টি = 540°

 সুতরাং   80° + 130° + 120° + 110° + x = 540°

বা,   440° + x = 540°

বা,    x = 540° - 440° = 100°

21) সুষম ষড়ভুজের প্রতিটি বহিঃস্থ এবং প্রতিটি অন্তঃস্থ কোণের মান কত?

Ans : আমরা জানি, কোন বহুভুজের বহিঃস্থ কোণগুলোর সমষ্টি 360°

 সুতরাং সুষম ষড়ভুজের প্রতিটি বহিঃস্থ  কোণ =  360°/6 = 60°

এবং প্রতিটি অন্তঃস্থ  কোণ = 180° -  60° =  120° 

[ কারণ, যে কোন বহুভুজের একটি অন্তঃস্থ কোন সংলগ্ন একটি বহিঃস্থ কোণের সমষ্টি =  180° ]

22) সুষম অষ্টভুজের প্রতিটি বহিঃস্থ এবং প্রতিটি অন্তঃস্থ কোণের মান কত?

Ans : আমরা জানি, কোন বহুভুজের বহিঃস্থ কোণগুলোর সমষ্টি = 360°

 সুতরাং সুষম অষ্টভুজের প্রতিটি বহিঃস্থ  কোণ =  360°/8 = 45°

এবং প্রতিটি অন্তঃস্থ  কোণ = 180° -  45° =  135° 

[ কারণ, যে কোন বহুভুজের একটি অন্তঃস্থ কোন সংলগ্ন একটি বহিঃস্থ কোণের সমষ্টি =  180° ]

23) সুষম 20 ভুজের প্রতিটি বহিঃস্থ এবং প্রতিটি অন্তঃস্থ কোণের মান কত?

Ans : আমরা জানি, কোন বহুভুজের বহিঃস্থ কোণগুলোর সমষ্টি = 360°

 সুতরাং সুষম 20 ভুজের প্রতিটি বহিঃস্থ  কোণ =  360°/20 = 18°

এবং প্রতিটি অন্তঃস্থ  কোণ = 180° -  18° =  162° 

[ কারণ, যে কোন বহুভুজের একটি অন্তঃস্থ কোন সংলগ্ন একটি বহিঃস্থ কোণের সমষ্টি =  180° ]

24) একটি সুষম বহুভুজের একটি বহিঃস্থ কোণের মান 45° হলে তার বাহুর সংখ্যা কত?

Ans :  বাহুর সংখ্যা =  360°/একটি বহিঃস্থ কোণের মান = 360°/ 45° = 8

25) একটি সুষম বহুভুজের একটি অন্তঃস্থ কোণের মান 144° হলে তার বাহুর সংখ্যা কত?

Ans :  একটি সুষম বহুভুজের একটি অন্তঃস্থ কোণের মান 144°

 সুতরাং একটি সুষম বহুভুজের একটি বহিঃস্থ কোণের মান =   (180° -  144° ) =  36°

 সুতরাং  বাহুর সংখ্যা =  360°/একটি বহিঃস্থ কোণের মান = 360°/ 36° = 10 টি।

26) একটি ত্রিভুজের তিনটি বহিঃস্থ কোণ 125°, 125° , x হলে,  x-এর মান কত?

Ans : আমরা জানি, কোন বহুভুজের বহিঃস্থ কোণগুলোর সমষ্টি = 360°

 সুতরাং 125° + 125° +  x = 360°

বা,   250° +  x = 360°

 বা,   x = 360° - 250°  = 110° 

27) একটি সুষম বহুভুজের বাহুর সংখ্যা 15 হলে, তার প্রতিটি বহিঃস্থ কোণের মান কত?

Ans: প্রতিটি বহিঃস্থ কোণের =   360°/বাহুর সংখ্যা = 360°/15 = 24 

28) ট্রাপিজিয়াম কাকে বলে?

Ans : যে চতুর্ভুজের এক জোড়া বিপরীত বাহু সমান্তরাল তাকে ট্রাপিজিয়াম বলে।

29) সমদ্বিবাহু ট্রাপিজিয়াম কাকে বলে?

Ans : যদি একটি ট্রাপিজিয়ামের অসমান্তরাল বাহু দুটি সমান হয় তবে এরূপ ট্রাপিজিয়ামকে সমদ্বিবাহু ট্রাপিজিয়াম বলে।

30) RING সামান্তরিকের <R = 70° হলে, অন্য কোণ গুলোর মান কত?

Ans : সামান্তরিকের সন্নিহিত কোণের সমষ্টি 180° । 

সুতরাং  <R  + <I = 180°

বা,   <I = 180° - 70°  [ যেহেতু <R = 70° ]

বা,  <I = 110° 

যেহেতু সামান্তরিকের বিপরীত কোণগুলো সমান।

তাই  <R = <N = 70°

এবং  <I = <G = 110° 

31) ABCD সামন্তরিকের সন্নিহিত বাহু দুটি 12 সেন্টিমিটার এবং 7 সেন্টিমিটার। সামান্তরিকের পরিসীমা নির্ণয় কর?

Ans : আমরাজানি, সামান্তরিকের বিপরীত বাহুগুলো পরস্পর সমান।

সুতরাং AB = CD = 12 সেন্টিমিটার  এবং BC = AD = 7 সেন্টিমিটার।

সুতরাং পরিসীমা = AB + BC + CD + AD = 12 + 7 + 12 + 7 = 38 সেন্টিমিটার।

32) HELP একটি সামান্তরিকের কর্ণ দুটি O বিন্দুতে ছেদ করেছে। OE = 4 সেমি এবং HL হলো PE এর চেয়ে 5  সেমি বেশি। OH এর দৈর্ঘ্য কত? 

Ans : আমরা জানি, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।

OE = OP = 4 সেমি   

সুতরাং P E = 4+4 = 8 সেমি।

সুতরাং  HL =  ( 8 + 5 ) = 13 সেমি।

OH = 13/2 = 6.5 সেমি।

33) একটি আয়তক্ষেত্রের প্রতিটি কোণের মান সমান হলে,  তবে একটি কোণের মান কত?

Ans : আমরা জানি চতুর্ভুজের চারটি কোণের সমষ্টি = 360°

সুতরাং একটি কোণের মান = 360°/4 = 90°